AVL树和红黑树

Posted on Edited on In Word count in article: 3k Reading time ≈ 3 mins.
go的AVL树实现，红黑树

AVL树（平衡二叉搜索树）

基于作者名字命名

平衡因子： 某个结点的左子树的高度减去右子树的高度得到的差值

AVL树的特点：
1、左右子树的高度差的绝对值小于1，即平衡因子{-1,0,1}
2、其每一颗子树均为平衡二叉树

节点会储存额外的信息

1
2
3
4
5
6
type AVLTreeNode struct {
    value int
    high  int
    left  *AVLTreeNode
    right *AVLTreeNode
}

AVL树具有监督机制：树的某一部分的不平衡度超过平衡因子后触发相应的平衡操作。保证树的平衡度在平衡因子范围内

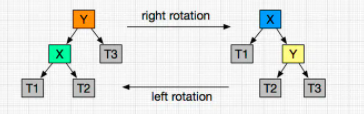
通过左旋、右旋操作，分为四种情况

单次左右旋， 注意旋转的与被旋转的节点更换

1

双次旋转

2

case2情况下，需要先对y结点进行一次左旋转，然后再对z结点进行一次右旋转
case3情况下，需要先对y结点进行一次右旋转，然后再对z结点进行一次左旋转

实现AVL树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
// 树节点
type AVLTreeNode struct {
    value int   // 节点值
    high  int   // 节点高度，最底层新插入的高度是0
    left  *AVLTreeNode
    right *AVLTreeNode
}
// 初始化一个AVL树
func NewAVLTreeRoot(root int) *AVLTreeNode {
    return &AVLTreeNode{root, 0, nil, nil}
}
// 插入节点
func (this *AVLTreeNode) InsertNode(v int) *AVLTreeNode {
    // 到叶子节点为nil时，插入v的值，递归终止条件
    if this == nil {
        return &AVLTreeNode{v, 0, nil, nil}
    }
    // v小于当前节点的value，左子树往下
    if v < this.value {
        // 左节点往下插入。开始递归，最终得到要插入的节点，就是this.left
        // 到最底层，此时的this是插入后的新节点的父节点，开始向上递归平衡
        this.left = this.left.InsertNode(v)
        // 开始回溯时，从倒数第二层开始向上，更新新节点的父节点得到的高度
        this.high = getMax(this.left.getNodeHigh(), this.right.getNodeHigh()) + 1
        // 检查高度差，高度差为2则复发平衡，触发第一次回溯时候就是新插入的节点的父父节点
        if this.left.getNodeHigh()-this.right.getNodeHigh() == 2 {
            // 如果要插入的值小于当前节点左节点的值，则右旋，否则 左右旋
            if v < this.left.value {
                return this.rightRotation()
            } else {
                return this.leftRightRotation()
            }
        }
    // 与上面相反，插入的时候左右交替比较插入，回溯的时候也是左右交替回溯
    } else {
        this.right = this.right.InsertNode(v)
        this.high = getMax(this.left.getNodeHigh(), this.right.getNodeHigh()) + 1
        if this.right.getNodeHigh()-this.left.getNodeHigh() == 2 {
            if v < this.right.value {
                return this.rightLeftRotation()
            } else {
                return this.leftRotation()
            }
        }
    }
    return this
}
// 左旋
func (this *AVLTreeNode) leftRotation() *AVLTreeNode {
    // 更换节点
    node := this.right
    this.right = node.left
    node.left = this
    // 更新高度
    this.high = getMax(this.left.getNodeHigh(), this.right.getNodeHigh()) + 1
    node.high = getMax(node.left.getNodeHigh(), node.right.getNodeHigh()) + 1
    return node
}

// 右旋
func (this *AVLTreeNode) rightRotation() *AVLTreeNode {
    node := this.left
    this.left = node.right
    node.right = this
    this.high = getMax(this.left.getNodeHigh(), this.right.getNodeHigh()) + 1
    node.high = getMax(node.left.getNodeHigh(), node.right.getNodeHigh()) + 1
    return node
}

// 左右旋
func (this *AVLTreeNode) leftRightRotation() *AVLTreeNode {
    this.left = this.left.leftRotation()
    return this.rightRotation()
}

// 右左旋
func (this *AVLTreeNode) rightLeftRotation() *AVLTreeNode {
    this.right = this.right.rightRotation()
    return this.leftRotation()
}

// 获取节点高度
func (this *AVLTreeNode) getNodeHigh() int {
    if this == nil {
        return -1
    }
    return this.high
}
// 获取最大值
func getMax(a, b int) int {
    if a > b {
        return a
    }
    return b
}

红黑树

红黑树是一种自平衡的二叉搜索树，它包含了二叉搜索树的特性，同时具备以下性质：

1、所有节点的颜色不是红色就是黑色。
2、根节点是黑色。
3、每个叶子节点都是黑色的空节点(nil)。
4、每个红色节点的两个子节点都是黑色。(从每个叶子到根节点的所有路径上不能有两个连续的红色节点)
5、从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点

与AVL树相比，没有AVL树那么严格的自平衡，允许比较大的平衡因子

查询多，更新少的用AVL， 更新多一点的用红黑树