数组、链表和跳表

Posted on Edited on In Word count in article: 1.9k Reading time ≈ 2 mins.
数组，链表，跳表，时间复杂度，空间复杂度

线性表

线性表是最常用且最简单的一种数据结构，它是n个数据元素的有限序列。

实现线性表的方式一般有两种，一种是使用数组存储线性表的元素，即用一组连续的存储单元依次存储线性表的数据元素。另一种是使用链表存储线性表的元素，即用一组任意的存储单元存储线性表的数据元素（存储单元可以是连续的，也可以是不连续的）

数组

golang 数组 slice

1
var a []int

每当申请数组时，计算机在内存中开辟了一段连续的地址，每一个地址直接可以通过内存管理器进行访问

所以无论访问哪个元素，时间复杂度是一样的，常数O(1)的

添加，删除时的操作，插入，删除元素都需要移动后面的元素，复杂度是O(n)

prepend: O(1), append: O(1), insert：O(n), del: O(n), lookup:O(1)

prepend正常情况下是O(n),可以特殊化到O(1)，申请稍大一些的内存空间，在前面预留一些，操作的时候把头下标前移一个位置即可

1

空间复杂度

O(n)

链表

1.每个元素有Value、Next，next指向下一个元素

2.头指针用head表示，尾指针用tail表示

3.最后一个元素next指向空

4.增加或删除节点的话，没有引起整个链表的群移操作，也不需要复制元素，挪动元素到新的位置，所以它移动的效率和修改的操作效率非常高，复杂度为O(1)

5.这个结构导致了访问链表中的任何一个位置，操作就不再简单了，复杂度为O(n)

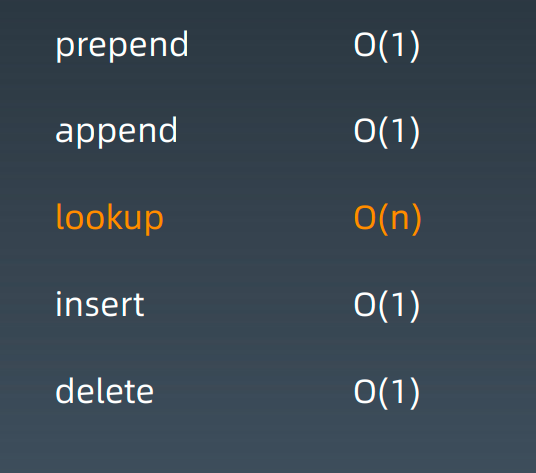
prepend: O(1), append: O(1), insert：O(1), del: O(1), lookup:O(n)

5

2

空间复杂度

O(n)

单链表

1
2
3
4
5
// ListNode ...
type ListNode struct {
    Val int
    Next *ListNode
}

由各个内存结构通过一个 Next 指针链接在一起组成，每一个内存结构都存在后继内存结构【链尾除外】，内存结构由数据域和 Next 指针域组成

1.Data 数据 + Next 指针，组成一个单链表的内存结构

2.第一个内存结构称为 链头，最后一个内存结构称为 链尾

3.链尾的 Next 指针设置为 NULL [指向空]

4.单链表的遍历方向单一【只能从链头一直遍历到链尾】

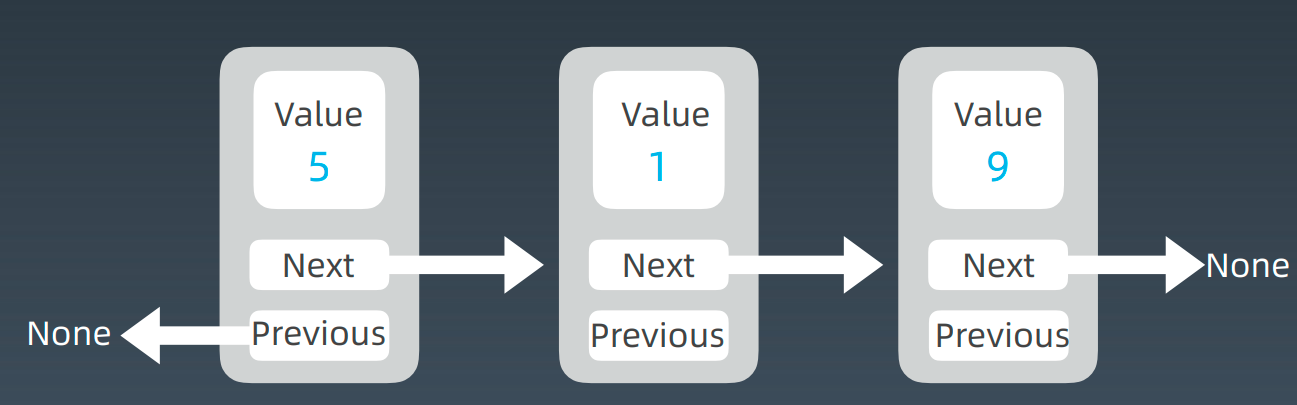
双向链表

1
2
3
4
5
6
7
// DNode ...
type DNode struct {
	data interface{}
	prev *DNode
	next *DNode
}

由各个内存结构通过指针 Next 和指针 Prev 链接在一起组成，每一个内存结构都存在前驱内存结构和后继内存结构【链头没有前驱，链尾没有后继】，内存结构由数据域、Prev 指针域和 Next 指针域组成

1.Data 数据 + Next 指针 + Prev 指针，组成一个双向链表的内存结构

2.第一个内存结构称为 链头，最后一个内存结构称为 链尾

3.链头的 Prev 指针设置为 NULL， 链尾的 Next 指针设置为 NULL

4.Prev 指向的内存结构称为 前驱， Next 指向的内存结构称为 后继

5.双向链表的遍历是双向的，即如果把从链头的 Next 一直到链尾的[NULL] 遍历方向定义为正向，那么从链尾的 Prev 一直到链头 [NULL ]遍历方向就是反向

循环链表

在单向链表和双向链表的基础上

单向循环链表 [Circular Linked List] : 由各个内存结构通过一个指针 Next 链接在一起组成，每一个内存结构都存在后继内存结构，内存结构由数据域和 Next 指针域组成。

双向循环链表 [Double Circular Linked List] : 由各个内存结构通过指针 Next 和指针 Prev 链接在一起组成，每一个内存结构都存在前驱内存结构和后继内存结构，内存结构由数据域、Prev 指针域和 Next 指针域组成。

1.循环链表分为单向、双向两种

2.单向的实现就是在单链表的基础上，把链尾的 Next 指针直接指向链头，形成一个闭环

3.双向的实现就是在双向链表的基础上，把链尾的 Next 指针指向链头，再把链头的 Prev 指针指向链尾，形成一个闭环

4.循环链表没有链头和链尾的说法，因为是闭环的，所以每一个内存结构都可以充当链头和链尾

跳表

链表在增加删除都很快，都是O(1)操作

但是查询很慢，是O(n)那么如何给链表的查询加速呢

升维

增加多级索引

3

由于节点的增删改查，会导致索引不工整，维护成本相对较高。

在redis里面，就是使用的跳表。

时间复杂度

4

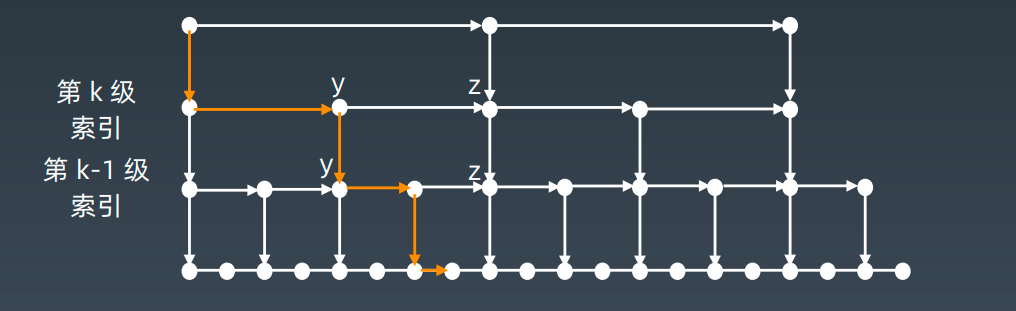
索引的高度：logn，每层索引遍历的结点个数：3

在跳表中查询任意数据的时间复杂度就是 O(logn)

空间复杂度

O(n)

每层节点，每两个节点抽1个 n/2, 每3个节点抽一个 3/n