树，二叉树，二叉搜索树专题

Posted on Edited on In Word count in article: 10k Reading time ≈ 9 mins.
树相关的基本概念，以及python，go下的树模板

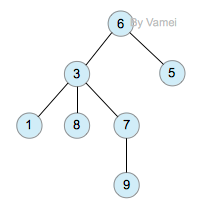
树

树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根

1

树的深度为层次数

  1. 树是元素的集合。

  2. 该集合可以为空。这时树中没有元素，我们称树为空树 (empty tree)。

  3. 如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连

树的实现：
每个节点储存元素和多个指向子节点的指针。然而，子节点数目是不确定的。一个父节点可能有大量的子节点，而另一个父节点可能只有一个子节点，而树的增删节点操作会让子节点的数目发生进一步的变化。这种不确定性就可能带来大量的内存相关操作，并且容易造成内存的浪费

二叉树与二叉搜索树

二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点

由于二叉树的子节点数目确定，所以可以直接采用上图方式在内存中实现。每个节点有一个左子节点(left children)和右子节点(right children)。左子节点是左子树的根节点，右子节点是右子树的根节点。

如果我们给二叉树加一个额外的条件，就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。二叉搜索树要求：每个节点都不比它左子树的任意元素小，而且不比它的右子树的任意元素大。

二叉搜索树可以方便的实现搜索算法。在搜索元素x的时候，我们可以将x和根节点比较:

  1. 如果x等于根节点，那么找到x，停止搜索 (终止条件)

  2. 如果x小于根节点，那么搜索左子树

  3. 如果x大于根节点，那么搜索右子树

二叉搜索树所需要进行的操作次数最多与树的深度相等。n个节点的二叉搜索树的深度最多为n，最少为log(n)

树模板

python

1
2
3
4
5
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

Go

1
2
3
4
5
type TreeNode struct {
      Val int
      Left *TreeNode
      Right *TreeNode
  }

例题

前序遍历

根左右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

//preorderTraversal 前序遍历，递归方法，时间O(n),空间O(n)
func preorderTraversal(root *TreeNode) []int {
    res := []int{}
    var handle func(*TreeNode)
    handle = func(root *TreeNode) {
        if root == nil {
            return
        }
        res = append(res, root.Val)
        handle(root.Left)
        handle(root.Right)
    }
    handle(root)
    return res
}

// preorderTraversal 迭代法，手动维护一个栈， 时间O(n),空间O(n)
// 1.初始都为空
// 2.先加入值，根，然后根入栈，node=node.left
// 3.左边全入栈，并加入结果，
// 4.从下往上出栈，node=node.right
func preorderTraversal(root *TreeNode) []int {
    stack := []*TreeNode{}
    node := root
    res := []int{}

    for node != nil || len(stack) > 0 {
        for node != nil {
        	// 加入节点值
            res = append(res, node.Val)
            // 入栈
            stack = append(stack, node)
            // 根左右顺序
            node = node.Left
        }
        // 出栈，往右边走
        node = stack[len(stack) - 1].Right
        // 减小栈
        stack = stack[:len(stack) - 1]
    }
    return res
}

中序遍历

左根右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

//inorderTraversal 中序遍历，递归 时间O(n),空间O(n)
func inorderTraversal(root *TreeNode) []int {
    res := []int{}
    var handle func(*TreeNode)
    handle = func(root *TreeNode) {
        if root == nil {
            return
        }
        handle(root.Left)
        res = append(res, root.Val)
        handle(root.Right)
    }
    handle(root)
    return res 
}

// inorderTraversal 迭代法 时间O(n),空间O(n)
// 1.初始都为空
// 2.先根入栈，node=node.left
// 3.左边全入栈，没有加入结果，
// 4.从下往上出栈，出来的是左节点，加入结果 然后node=node.right
func inorderTraversal(root *TreeNode) []int {
   stack := []*TreeNode{}
   node := root
   res := []int{}

   for node != nil || len(stack) > 0 {
        // 先把左节点都入栈，左 根 右 顺序
       for node != nil {
           stack = append(stack, node)
           node = node.Left
        }
        // 出栈，将节点值加入结果
        node = stack[len(stack) - 1]
        stack = stack[:len(stack) - 1]
        res = append(res, node.Val)
        // 右边节点
        node = node.Right
   }
   return res
}

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
func postorderTraversal(root *TreeNode) []int {
    res := []int{}
    var handle func(root *TreeNode)
    handle = func(root *TreeNode) {
        if root == nil {
            return
        }
        handle(root.Left)
        handle(root.Right)
        res = append(res, root.Val)
    }
    handle(root)
    return res
}

// 迭代后序遍历
// 遍历本质就是内存的访问顺序，可以通过前序根左右变成根右左，再反转，但是不符合遍历本质
// 按照左右根的顺序，先把左节点都入栈，然后出栈取最下层的左节点，栈减少
// 判断这个节点的有节点是不是有值，没有的话就是最低左节点，加入结果，并标记当前节点
// 取其上一层的左节点继续，右节点有值，则遍历右节点，并标记
// 左右根，继续往上
// 1.初始都为空
// 2.先根入栈，node=node.left
// 3.左边全入栈，没有加入结果，
// 4.从下往上出栈，出来的是左节点
// 5.如果右节点不为空，则root=root.right  然后node=node.right
// 6.然后下一个循环，root.Right为空，基本都为空了，加入结果。并将root加入标记
// 7.继续出队
func postorderTraversal(root *TreeNode) []int {
    stack := []*TreeNode{}
    var prev *TreeNode
    res := []int{}

    for root != nil || len(stack) > 0 {
        for root != nil {
            stack = append(stack, root)
            root = root.Left
        }
        root = stack[len(stack) - 1]
        stack = stack[:len(stack) - 1]
        if root.Right == nil || root.Right == prev {
            res = append(res, root.Val)
            prev = root
            root = nil
        } else {
            stack = append(stack, root)
            root = root.Right
        }
    }
    return res
}

从前序中序构造二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

// buildTree 递归法
// 1.前序遍历的第一个节点，就是根节点，根左右，根节点后面跟的是左子树，然后是右子树
// 2.中序遍历的根节点在中间，根节点的位置左边就是左子树，右边就是右子树
// 3.因为都是一个树，所以中序和前序的左子树长度相等，同理右子树，所以中序的根节点以前长度在前序根节点以后的长度就是左子树
// 4.重复子问题就是，前序得到根节点，中序找到根节点，根节点之前就是左子树，左子树出左节点，根节点之后就是右子树，右子树出右节点
func buildTree(preorder []int, inorder []int) *TreeNode {
	// 终止条件，前序长度为0，说明已经递归完
    if len(preorder)==0{
        return nil
    }
    // 前序的第一个节点就是根节点
    root:=&TreeNode{
        Val:preorder[0],
    }
    // 找到根节点在中序的位置
    var num int
    for k, v := range inorder{
        if v == preorder[0]{
            num = k
            break
        }
    }
    // 处理左右子树，前序是出去第一个元素，包含num的元素，中序是包含第一个元素，不包含num的元素
    root.Left = buildTree(preorder[1:num+1],inorder[:num])
    root.Right = buildTree(preorder[num+1:],inorder[num+1:])
    return root
}

N叉树的前序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
type Node struct {
    Val int
    Children []*Node
}
 
var res []int

//preorder 递归方法
func preorder(root *Node) []int {
    // 重置
    res = []int{}
    handle(root)
    return res
}

// 递归函数
func handle(root *Node) {
    if root != nil {
        res = append(res, root.Val)
        // 子节点
        for _, v := range root.Children {
            handle(v)
        }
    }
}

//preorder 迭代法
func preorder(root *Node) []int {
    var res []int
    // 辅助栈
    var stack = []*Node{root}
    for 0 < len(stack) {
        // 节点遍历，for更新root
        for root != nil {
            //前序输出，根左右，将根节点加入结果
            res = append(res, root.Val)
            // 子节点为0，就跳出循环
            if 0 == len(root.Children) {
                break
            }
            // 遍历子节点，子节点入栈，当做下次循环的根节点，倒序加入，不加入第一个，栈先入后出
            for i := len(root.Children) - 1; 0 < i; i-- {
                stack = append(stack, root.Children[i]) //入栈
            }
            // 更新root，为子节点的第一个，根->左
            root = root.Children[0]
        }
        // 没有子节点则跳出循环，出栈，最底层的右，根->左->右
        root = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
    }
    return res
}

func preorder(root *Node) []int {
    res := []int{}
    if root == nil {
        return res
    }
    stack := []*Node{root}

    for len(stack) > 0 {
        node := stack[len(stack) - 1]
        stack  = stack[:len(stack) - 1]
        res = append(res, node.Val)
        for i := len(node.Children) - 1; i >= 0; i-- {
            stack = append(stack, node.Children[i])
        }
    }
    return res
}

二叉树的最近公共祖先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

// lowestCommonAncestor 递归方法
// 转化为最小重复子问题，根左右节点的几种情况如下：
// 1.若root中只包含p则返回p
// 2.若root中只包含q则返回q
// 3.若root中不包含p也不包含q则返回NULL
// 4.若root中同时包含p和q，则返回root（此时root为最近公共祖先）
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    // 不同层。，如果该节点找到了p，q则返回该节点
    if root == nil || p == root || q == root {
        return root
    }
    // 递归就是判断当前节点是不是等于p或q，不是就一直往下找，找到就返回，或者找到nil也返回
    left := lowestCommonAncestor(root.Left, p, q)
    right := lowestCommonAncestor(root.Right, p, q)
    // 如果存在nil则向上返回另一个节点
    if left == nil {
        return right
    }
    if right == nil {
        return left
    }
    // 左右不等于nil，说明左右等于p，q，则root根就是最近公共祖先
    return root
}

// lowestCommonAncestor 递归+迭代法
// 1.通过递归遍历，记录所有父节点
// 2.通过map记录p节点的访问路径
// 3.然后看另一节点是否有相同的父节点，有为最近公共祖先
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    // 用于记录所有的父节点路径
    parent := map[int]*TreeNode{}
    // 用于记录p节点的访问路径，并判断q的相同父节点
    visited := map[int]bool{}
    // 递归遍历树，只记录父节点
    var dfs func(*TreeNode)
    dfs = func(r *TreeNode) {
        if r == nil {
            return
        }
        // 只看左右节点是否为空，因为只记录父节点
        if r.Left != nil {
            parent[r.Left.Val] = r
            dfs(r.Left)
        }
        if r.Right != nil {
            parent[r.Right.Val] = r
            dfs(r.Right)
        }
    }
    dfs(root)

    // 记录p节点的访问路径，从下向上
    for p != nil {
        visited[p.Val] = true
        p = parent[p.Val]
    }
    // 看另一节点是否有相同值，有则返回就是结果
    for q != nil {
        if visited[q.Val] {
            return q
        }
        q = parent[q.Val]
    }

    return nil
}

二叉树的最大深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

// 层序遍历求最大深度
func maxDepth(root *TreeNode) int {
    var res int
    if root == nil {
        return res
    }
    var dfs func(*TreeNode, int)
    dfs = func(root *TreeNode, l int) {
        if l == res {
            res++
        }
        if root.Left != nil { dfs(root.Left, l+1) }
        if root.Right != nil { dfs(root.Right, l+1) }
    }
    dfs(root, 0)
    return res
}

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    q := []*TreeNode{root}
    res := 0

    for len(q) > 0 {
        l := len(q)
        for l > 0 {
            node := q[0]
            q = q[1:]
            if node.Left != nil {
                q = append(q, node.Left)
            }
            if node.Right != nil {
                q = append(q, node.Right)
            }
            l--
        }
        res++
    }
    return res
}

N叉树的层序遍历

第一层循环的是每一层，获取当前层的长度，初始化临时结果，然后下一层遍历这个结果

然后出队，取出节点，遍历节点的children下一层，下一层的入队，上一层会遍历完按顺序出队

下一层的都入队之后，上一层的都出队，加入结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
// levelOrder 迭代法， 队列实现
func levelOrder(root *Node) [][]int {
    var res [][]int
    if root == nil {
        return res
    }
    // 初始化队列，将根节点加入
    q := []*Node{root}

    for len(q) > 0 {
    	// 记录当前队列的长度
        l := len(q)
        levelRes := []int{}
        // 不断出队，遍历
        for l > 0 {
        	// 队首出队
            node := q[0]
            q = q[1:]
            // 遍历节点的子节点，下一层
            if len(node.Children) != 0 {
            	// 子节点入队，队尾入队
                for _, v := range node.Children {
                    q = append(q, v)
                }
            }
            // 出队，记录值，放入结果，这是一层的结果
            levelRes = append(levelRes, node.Val)
            l--
        }
    // 将每一层的结果放入最终结果
    res = append(res, levelRes)
    }
    return res 
}

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func levelOrder(root *Node) [][]int {
    res := [][]int{}

    var dfs func(int, *Node)
    dfs = func(l int, root *Node) {
        // 先加层，相等时候加一个，加入之后就大于了，只有到下一层才继续加
        // 没有终止条件
        if l == len(res) {
            res = append(res, []int{})
        }
        // 每层加入值
        res[l] = append(res[l], root.Val)
        // 终止条件是root.Children为nil，不再遍历了
        for i := 0; i < len(root.Children); i++ {
            dfs(l+1, root.Children[i])
        }
    }
    // 初始递归从0开始
    if root != nil {
        dfs(0, root)
    }
    
    return res 
}

二叉树的层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// dfs 递归，注意判断递归终止条件，层序终止条件，是节点为nil，进入下层遍历要判断节点不是nil
func levelOrder(root *TreeNode) [][]int {
    res := [][]int{}
    if root == nil {
        return res
    }

    var dfs func(*TreeNode, int)
    dfs = func(root *TreeNode, l int) {
        if l == len(res) {
            res = append(res, []int{})
        }
        res[l] = append(res[l], root.Val)
        if root.Left != nil {dfs(root.Left, l+1)}
        if root.Right != nil {dfs(root.Right, l+1)}
    }
    dfs(root, 0)
    return res
}

// 别忘了判断nil，添加队列时候判断
func levelOrder(root *TreeNode) [][]int {
    res := [][]int{}
    if root == nil {
        return res
    }
    q := []*TreeNode{root}

    for len(q) > 0 {
        l := len(q)
        lCur := []int{}
        for i := 0; i < l; i++ {
            node := q[0]
            q = q[1:]
            lCur = append(lCur, node.Val)
            if node.Left != nil {q = append(q, node.Left)}
            if node.Right != nil {q = append(q, node.Right)}
        }
        res = append(res, lCur)
    }
    return res
}