斐波那契数列

Posted on Edited on In Word count in article: 3.3k Reading time ≈ 3 mins.
斐波那契数列，普通计算方式，递归，相关复杂度优化， 爬楼梯问题，动态规划，最小花费爬楼梯

Fib

0, 1, 1, 2, 3, 5, 8, 13, 21 ……

数学公式： F(n) = F(n - 1) + F(n - 2)

爬楼梯问题

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

类似：青蛙跳台阶

方法

动态规划

f(x)=f(x−1)+f(x−2)

每次只能爬1级或2级，所以f(x)只能从f(x−1)和f(x−2)转移过来，而这里要统计方案总数，我们就需要对这两项的贡献求和。

以上是动态规划的转移方程，下面我们来讨论边界条件。我们是从第0级开始爬的，所以从第0级爬到第0级我们可以看作只有一种方案，即f(0)=1从第0级到第1级也只有一种方案，即爬一级，f(1)=1。这两个作为边界条件就可以继续向后推导出第n 级的正确结果。我们不妨写几项来验证一下，根据转移方程得到f(2)=2，f(3)=3，f(4)=5……我们把这些情况都枚举出来，发现计算的结果是正确的。

符合斐波那契数列规律,这里形成的数列正好是斐波那契数列，答案要求的f(n 即是斐波那契数列的第n项（下标从0开始）

我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是(n) 的实现，但是由于这里的f(x) 只和f(x−1)与f(x−2) 有关，所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)

列表

1
2
3
4
5
6
7
8
9
func Fib(n int) []int {
  dp := make([]int, n+1)
  dp[0] = 1
  dp[1] = 1
  for i:=2; i<=n; i++ {
    dp[i] = dp[i-2] + dp[i-1]
  }
  return dp
}

时间复杂度：O(n)
空间复杂度：O(n)

常数(优化)

1
2
3
4
5
6
7
8
9
func Fib(n int) int {
    p, q, r := 0, 0, 1
    for i := 1; i <= n; i++ {
        p = q
        q = r
        r = p + q
    }
    return r
}

用常数作辅助中间变量，时间复杂度为O(n),空间复杂度为(1)

该方法适用于n比较小的时候，n比较大的时候，复杂度就会比较高

递归方法

直接递归

直接利用斐波那契公式即可

1
2
3
4
5
6
func Fib(i int) int {
	if i <= 2 {
		return i
	}
	return Fib(i-1) + Fib(i-2)
}

递归方法虽然可以得到斐波那契数列，但是分析它的时间复杂度，

画出递归树(状态树)

1

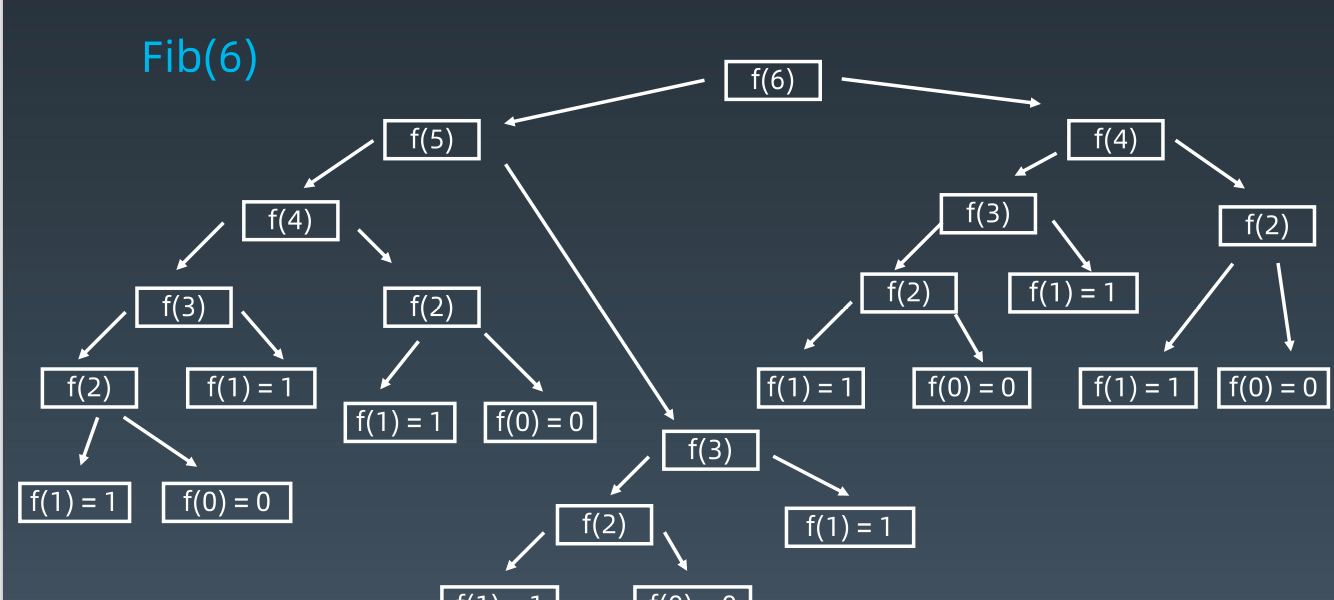
直接递归的时间复杂度是2^n次方
空间复杂度为递归深度是O(n)
可以发现有很多重复的计算部分，有些结果不只计算了一次

记忆化递归

将中间结果进行缓存,可以加速程序执行

1
2
3
4
5
6
7
8
var a = map[int]int{1:1,2:2}

func Fib(n int, a map[int]int) int {
  if _, ok := a[n]; !ok {
    a[n] = Fib(n-1, a) + Fib(n-2, a)
  }
  return a[n]
}

申请了一块长度为n的map
所以
时间复杂度:O(n)
空间复杂度:O(n)
相比直接递归，缩短了程序执行时间

最小花费爬楼梯

数组的每个索引作为一个阶梯，第 i个阶梯对应着一个非负数的体力花费值 costi。

每当你爬上一个阶梯你都要花费对应的体力花费值，然后你可以选择继续爬一个阶梯或者爬两个阶梯。

您需要找到达到楼层顶部的最低花费。在开始时，你可以选择从索引为 0 或 1 的元素作为初始阶梯。

动态规划解法

解法一

理解：
第i级台阶是第i-1级台阶的阶梯顶部。
踏上第i级台阶花费cost[i]，直接迈一大步跨过而不踏上去则不用花费。

2

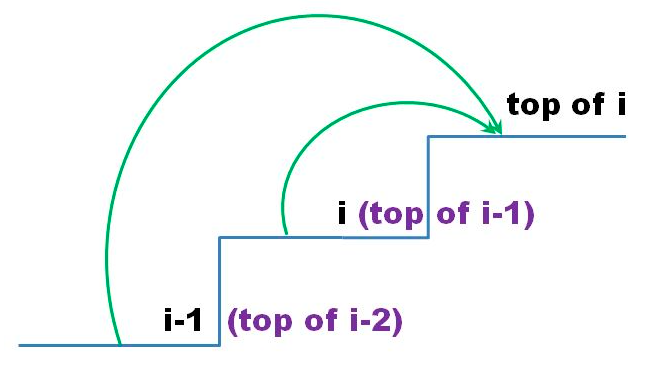
到达第i级台阶的阶梯顶部的最小花费，有两个选择：

1、从i往上到达i的顶部，花费为:到达第i的花费cost[i] + 到达i-1的最小花费minCost[i-1]
2、从i往上到达i的顶部，花费为:到达第i-1的花费cost[i-1] + 到达i-2的最小花费minCost[i-2]

从i往上到达i的顶部，需要花费minCost[i]

则为上面两种情况的最小值

minCost[i] = min(cost[i-1] + minCost[i-2], cost[i] + minCost[i-1])

则往前递推，归纳法，这是为n的情况，从0,1的情况开始， -1为地面，花费为0
minCost[0] = min(cost[-1], cost[0]) = min(0, cost[0]) = 0
minCost[1] = min(cost[0], cost[1])

python
1
2
3
4
5
6
7
8
class Solution(object):
    def minCostClimbingStairs(self, cost):
        n = len(cost)
        minCost = [0] * n
        minCost[1] = min(cost[0], cost[1])
        for i in range(2, n):
            minCost[i] = min(cost[i-1] + minCost[i-2], cost[i] + minCost[i-1])
        return minCost[-1]

解法二

相比于解法一，则往下挪了一阶梯，到达第i层，i到顶部不需要花费,或者从i-1到达顶部也不需要花费
则，最小花费为min(dp[i], dp[i-1]) + 0, 0为到达顶部的最小花费

3

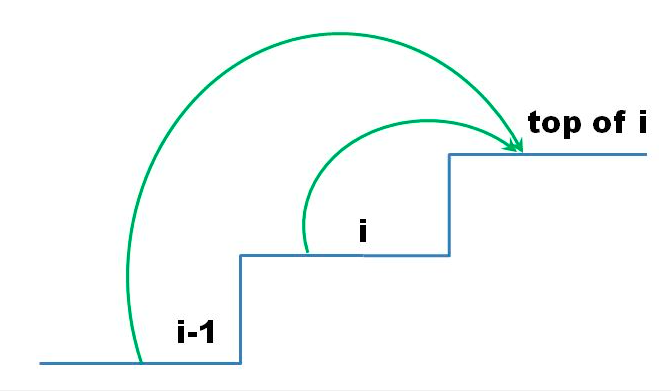
1、到达i阶，花费cost[i]
2、从i-1到达i阶:dp[i-1] + cpst[i]
3、从i-2到达i阶:dp[i-2] + cost[i]

则最小花费： dp[i] = min(dp[i-1] + dp[i-2]) + cost[i]

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def minCostClimbingStairs(self, cost):
        n = len(cost)
        dp[0] = [0] * n
        dp[0], dp[1] = cost[0], cost[1]
        for i in range(2, n):
            dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
        return min(dp[-2], dp[-1])

class Solution(object):
    def minCostClimbingStairs(self, cost):
        for i in range(2, len(cost)):
            cost[i] = min(cost[i-1], cost[i-2]) + cost[i]
        return min(cost[-2], cost[-1])

时间复杂度：O(n)，其中 n 是数组 cost 的长度。需要依次计算每个 dp 值，每个值的计算需要常数时间，因此总时间复杂度是 O(n)。

空间复杂度：O(n)。

解法三

使用滚动数组的思想，只需要使用有限的额外空间，优化空间复杂度为O[1]。

cost 的长度为 n，则 n 个阶梯分别对应下标 0 到 n−1，楼层顶部对应下标 n

则求达到下标n的花费，是cost[n-1]

创建长度为 n+1 的数组 dp，其中 dp[i] 表示达到下标 i 的最小花费

遍历到n+1

cost[(n+1)-1] 表示爬上i的花费

则到达第i阶的最小花费，为遍历 n+1 的数组 dp，for j ，往上要爬的j-1的花费，及爬上j-2的最小花费，与要爬上j-2的 花费，及爬j-3的最小花费

dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])

python
1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
    def minCostClimbingStairs(self, cost):
        # 指定当前阶的最小花费，pre表示地面-1， cur表示地面0
        pre, cur = 0, 0
        # 遍历到 len(cost)，即达到下标n
        for i in range(2, len(cost)+1):
           next = min(cost[i-1] + cur, cost[i-2] + pre)
           # pre就是差2阶到n阶之前的最小花费，cur就是差1阶到n之前的最小花费
           # 最后遍历完，cur = next就是最后的结果 
           pre, cur = cur, next
        return cur