时间复杂度与空间复杂度

算法

算法：解决特定问题的步骤的描述
特性：
—输入：有零个输入或者多个输
—输出：只有一个或者多个输出
—有穷型性：算法在执行有限个步骤时，会自动结束而不会陷入无限循环里面
—确定性：算法的每一步都有确定的含义而不会出现二义性
—可行性：算法的每一步都可以通过有限次数完成。

要求：
正确性、可读性、健壮性、时间效率高而且空间使用率低、简单性。
算法的复杂度分为时间复杂度和空间复杂度。

时间复杂度Big O Notation

时间复杂度实际上是一个函数，代表基本操作重复执行的次数，进而分析函数虽变量的变化来确定数量级，数量级用O表示

「 大O符号表示法 」，即 T(n) = O(f(n))

其中f(n) 表示每行代码执行次数之和，而 O 表示正比例关系，这个公式的全称是：算法的渐进时间复杂度

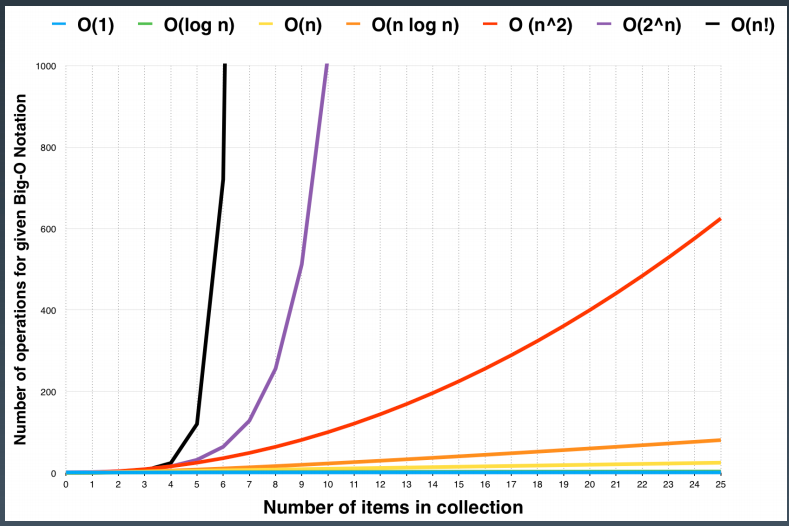
常见的时间复杂度量级有：

常数阶O(1)
对数阶O(logN)
线性阶O(n)
线性对数阶O(nlogN)
平方阶O(n²)
立方阶O(n³)
K次方阶O(n^k)
指数阶(2^n)

PS： 并列运行的为同级复杂度

空间复杂度

是对一个算法在运行过程中临时占用存储空间的度量，一个算法在计算机存储器上所占用的存储空间包括存储算法本身所占用的空间，算数和输入输出所占用的存储空间以及临时占用存储空间三个部分。

算法的输入输出数据所占用的存储空间是由待解决的问题来决定的，通过参数表由调用函数而来，它随本算法的不同而改变，存储算法本身所占用的存储空间有算法的书写长短成正比。算法在运行过程中占用的临时空间由不同的算法决定。

1、数组

2、递归深度